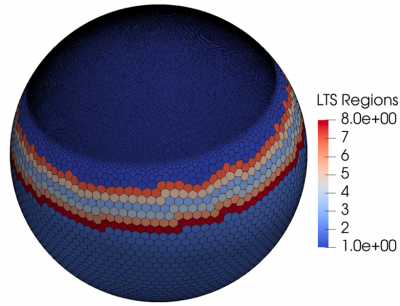
Local Time-Stepping: Matching Temporal Resolution to Spatial Resolution
The largest selectable time step, or time interval in a simulation, in standard time integration schemes is bounded above by the size of the smallest computational cell of the mesh. Using local time-stepping (LTS) allows researchers to select different time-steps for different regions of the mesh based on their cell size. This tool speeds up the simulation and allows finer high-resolution regions for the same computational cost as previous methods. Researchers developed an efficient parallel implementation process and assessed the performance of LTS schemes for the shallow water equations in the Model for Prediction Across Scales (MPAS).
Accurately simulating coastal physical processes, which need very high spatial resolution (i.e., the order of 1 km), greatly benefits from the use of LTS. Coastal processes are also influenced by far-away oceanic physics. LTS allows researchers to use different time steps in different regions of the globe to match their desired spatial resolution. This guarantees the required accuracy in regions of interest in a shorter amount of time without compromising the accuracy of the simulated solution far away from the coast.
To numerically solve equations on variable-resolution grids with regions of high spatial resolution, global time-stepping schemes employ the same small time step across the entire domain. This slows down the simulation. Researchers carried out an efficient parallel implementation and performance assessment of LTS schemes for the shallow water equations in MPAS, which is also used for ocean and climate simulations. These methods are fast, accurate, and scalable in a high-performance computing setting. Moreover, the scheme with convergence order three showed a reduction in terms of computational time of up to 70 percent compared to a Runge-Kutta scheme of order four on certain variable-resolution meshes.